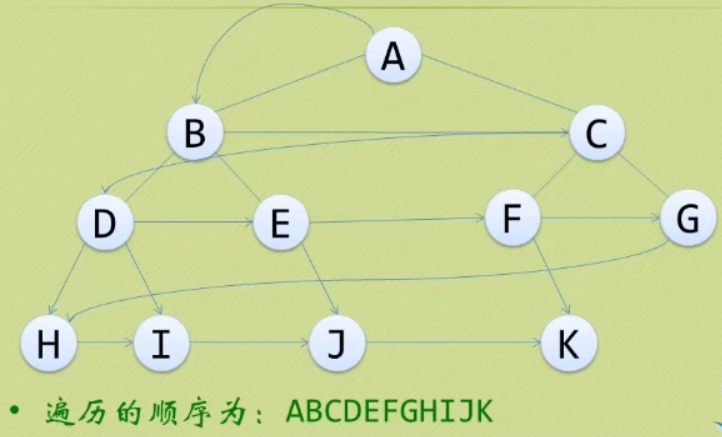
前面提到的链表、栈和队列都是一对一的线性结构,这节讲一对多的线性结构——树。
基本概念
「一对多」就是指一个元素只能有一个前驱,但可以有多个后继。
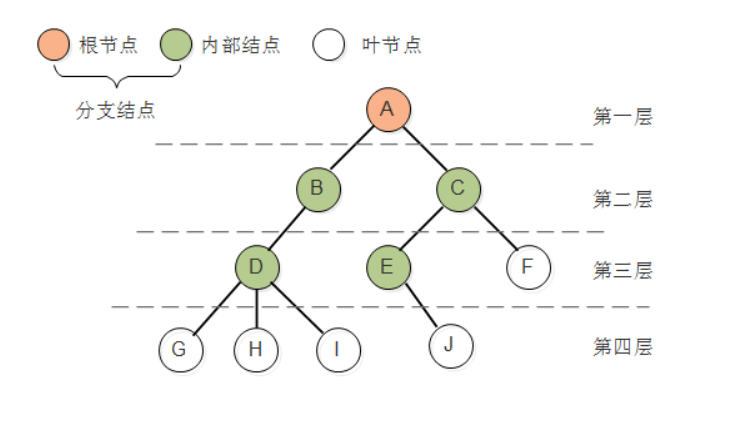
结点拥有的子树数被称为结点的度(Degree)。度为0的结点称为叶节点(Leaf)或终端结点,度不为0的结点称为分支结点。除根结点外,分支结点也被称为内部结点。结点的子树的根称为该结点的孩子(Child),该结点称为孩子的双亲或父结点。同一个双亲的孩子之间互称为兄弟。树的度是树中各个结点度的最大值。结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度(Depth)或高度。如果将树中结点的各个子树看成从左到右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。森林是m(m>=0)棵互不相交的树的集合。
-
二叉树 二叉树(Binary Tree)是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。
特点:
二叉树不存在度大于2的结点。
二叉树的子树有左右之分,次序不能颠倒。
-
斜树,满二叉树
斜树:所有的结点都只有左子树的二叉树叫左斜树。所有的结点都只有右子树的二叉树叫右斜树。这两者统称为斜树。斜树每一层只有一个结点,结点的个数与二叉树的深度相同。其实斜树就是线性表结构。
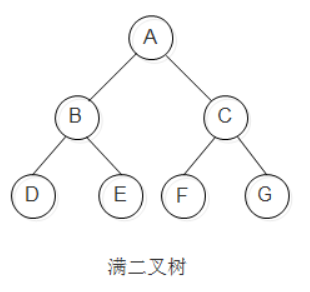
满二叉树:在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。 特点: 叶子只能出现在最下一层 非叶子结点的度一定是2 同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
-
完全二叉树,平衡二叉树
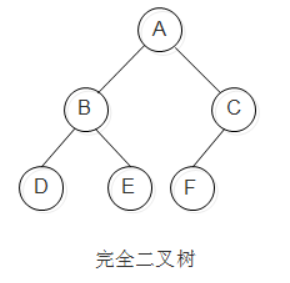
完全二叉树,若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。特点:
叶子结点只能出现在最下两层
最下层叶子在左部并且连续
同样结点数的二叉树,完全二叉树的深度最小
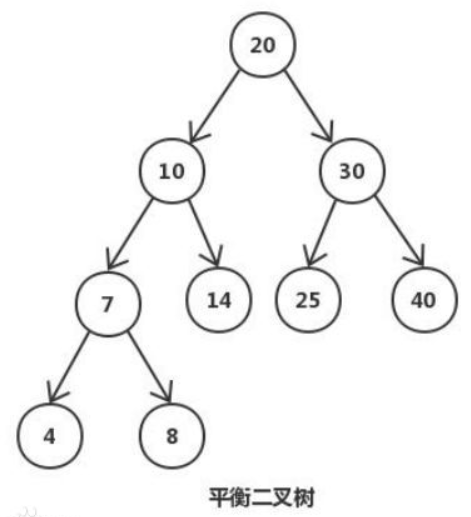
平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树非叶子节值大于左边子节点、小于右边子节点;没有值相等重复的节点;
-
红黑树
因为平衡二叉树
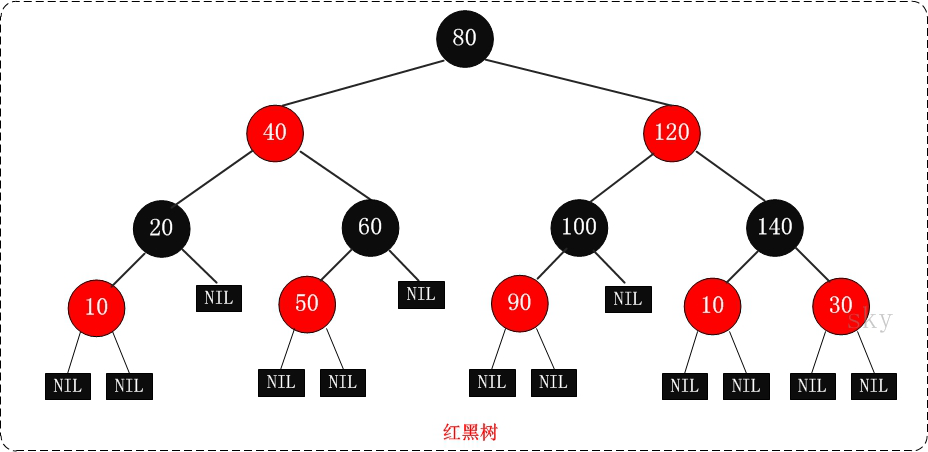
查询性能和树的层级(h高度)成反比,h值越小查询越快、为了保证树的结构左右两端数据大致平衡降低二叉树的查询难度一般会采用一种算法机制实现节点数据结构的平衡,实现了这种算法就有红黑树。红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。 例如,Java集合中的TreeSet和TreeMap。红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
-
B+树
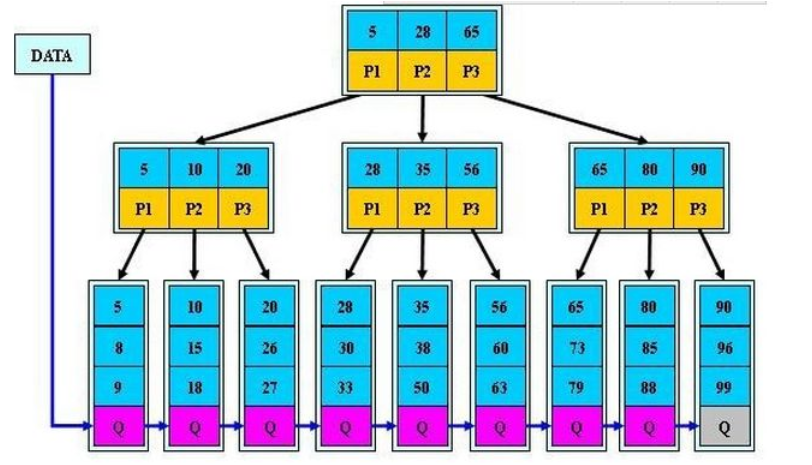
B+树充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。
例如MySQL的数据库索引查找:
B+树的非叶子节点不保存关键字记录的指针,这样使得B+树每个节点所能保存的关键字大大增加;
B+树叶子节点保存了父节点的所有关键字和关键字记录的指针,每个叶子节点的关键字从小到大链接;
B+树的根节点关键字数量和其子节点个数相等;
B+的非叶子节点只进行数据索引,不会存实际的关键字记录的指针,所有数据地址必须要到叶子节点才能获取到,所以每次数据查询的次数都一样;
- 二叉树遍历
前序遍历:先访问根结点,然后遍历左子树,最后遍历右子树。
中序遍历:先遍历左子树,然后遍历根结点,最后遍历右子树。
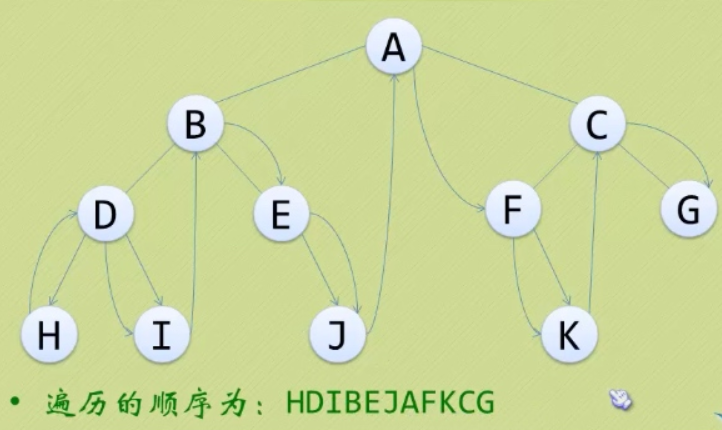
后序遍历:先遍历左子树,然后遍历右子树,最后遍历根结点。
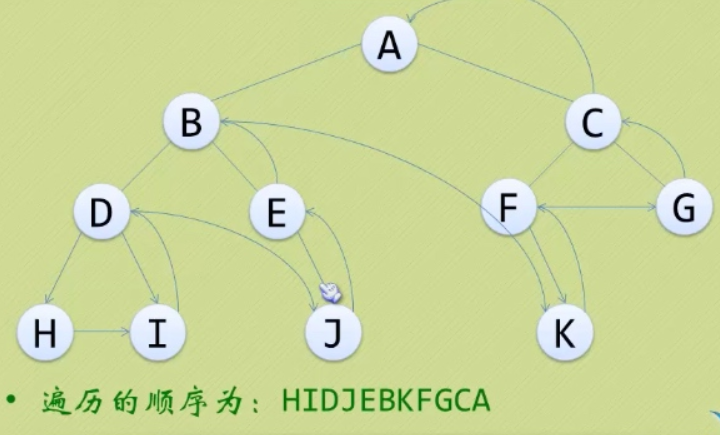
层次遍历:从上到下逐层遍历,在同一层中,按从左到右的顺序遍历。