图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的;其中,点通常被成为”顶点(vertex)”,而点与点之间的连线则被成为”边或弧”(edege)。通常记为,G=(V,E)。
概念
-
图分类
有向图和无向图
- 邻接点和度
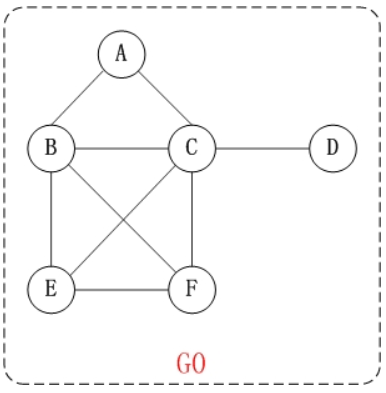
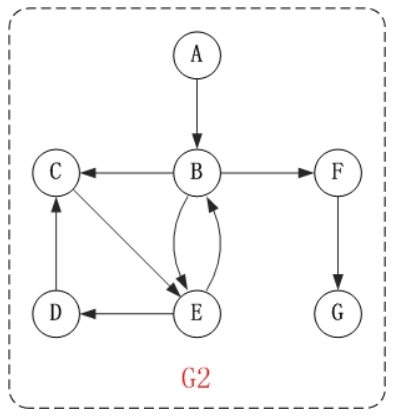
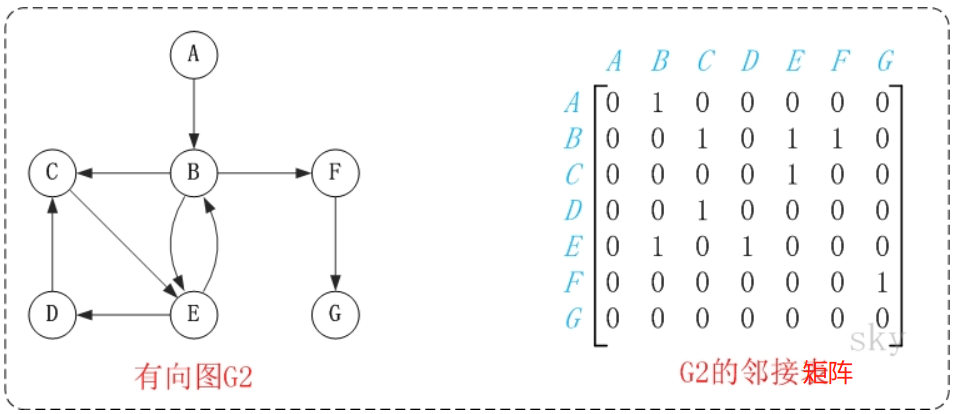
- 邻接点 一条边上的两个顶点叫做邻接点。 例如,上面无向图G0中的顶点A和顶点C就是邻接点。 在有向图中,除了邻接点之外;还有”入边”和”出边”的概念。 顶点的入边,是指以该顶点为终点的边。而顶点的出边,则是指以该顶点为起点的边。 例如,上面有向图G2中的B和E是邻接点;<B,E>是B的出边,还是E的入边。
- 度
在无向图中,某个顶点的度是邻接到该顶点的边(或弧)的数目。 例如,上面无向图G0中顶点A的度是2。
在有向图中,度还有”入度”和”出度”之分。 某个顶点的入度,是指以该顶点为终点的边的数目。而顶点的出度,则是指以该顶点为起点的边的数目。 顶点的度=入度+出度。 例如,上面有向图G2中,顶点B的入度是2,出度是3;顶点B的度=2+3=5。
-
图的存储结构
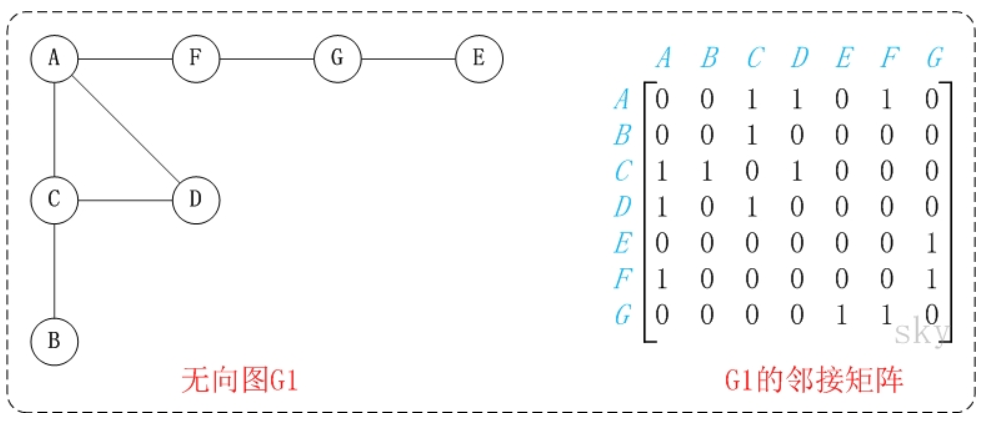
- 邻接矩阵 邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。 假设图中顶点数为n,则邻接矩阵定义为:

通常采用两个数组来实现邻接矩阵:一个一维数组用来保存顶点信息,一个二维数组来用保存边的信息。 邻接矩阵的缺点就是比较耗费空间。
- 邻接表
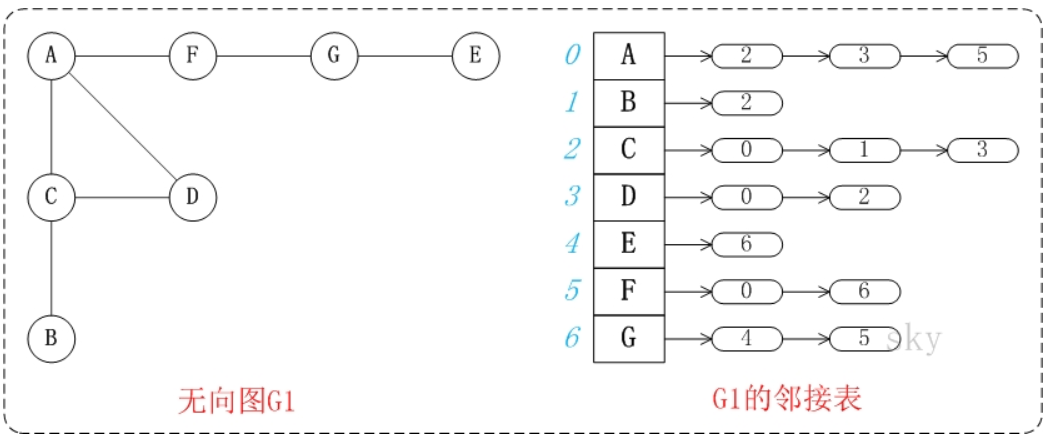
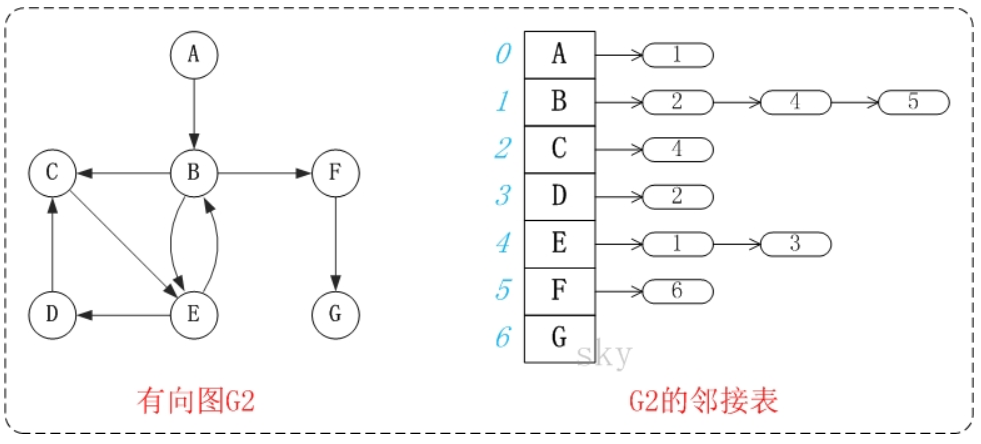
邻接表是图的一种链式存储表示方法。它是改进后的”邻接矩阵”,它的缺点是不方便判断两个顶点之间是否有边,但是相对邻接矩阵来说更省空间。
图的遍历
-
深度优先搜索
图的深度优先搜索(Depth First Search),和树的前序遍历比较类似。
它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
显然,深度优先搜索是一个递归的过程。
在此我想用一句话来形容 “一路走到头,不撞墙不回头”
-
广度优先遍历
广度优先搜索算法(Breadth First Search),又称为”宽度优先搜索”或”横向优先搜索”,简称BFS。
它的思想是:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远,依次访问和v有路径相通且路径长度为1,2…的顶点。
一层一层
实战
-
实战之Dijkstra最短路径算法
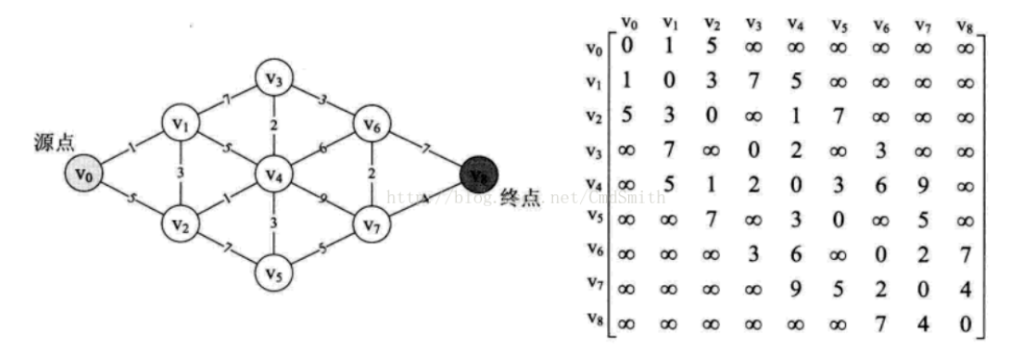
通过Dijkstra计算图G中的最短路径时,需要指定起点vs(即从顶点vs开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点,而U则是记录还未求出最短路径的顶点(以及该顶点到起点vs的距离)。
操作步骤:
(1) 初始时,S只包含起点vs;U包含除vs外的其他顶点,且U中顶点的距离为”起点vs到该顶点的距离”[例如,U中顶点v的距离为(vs,v)的长度,然后vs和v不相邻,则v的距离为∞]。
(2) 从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点vs的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(vs,v)的距离可能大于(vs,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。

-
实战之Prim与Kruskal最小生成树算法
- 最小生成树
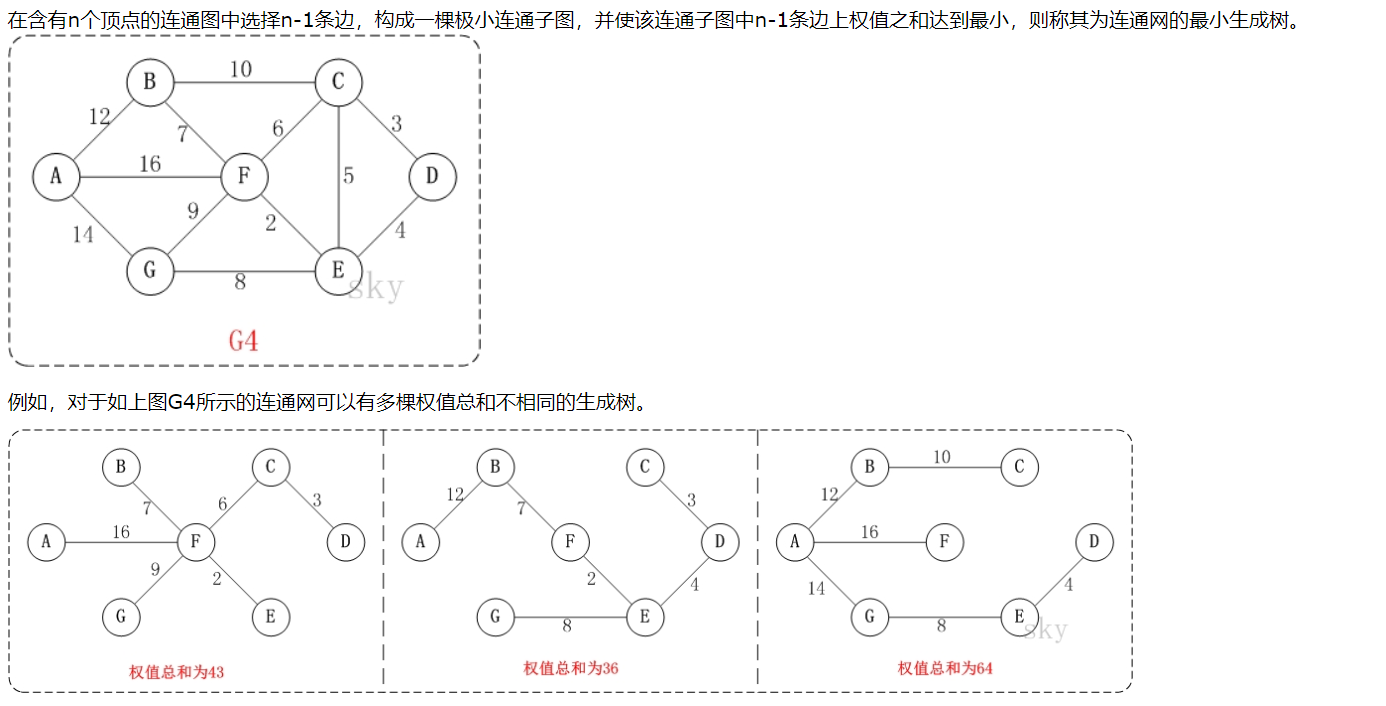
- Prime算法
基本思想 对于图G而言,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。 从所有uЄU,vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v),将顶点v加入集合U中,将边(u, v)加入集合T中,如此不断重复,直到U=V为止,最小生成树构造完毕,这时集合T中包含了最小生成树中的所有边。

- Kruskal算法
基本思想:按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路。 具体做法:首先构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中,并使森林中不产生回路,直至森林变成一棵树为止。

-
实战之Ford-Fulkerson最大流算法
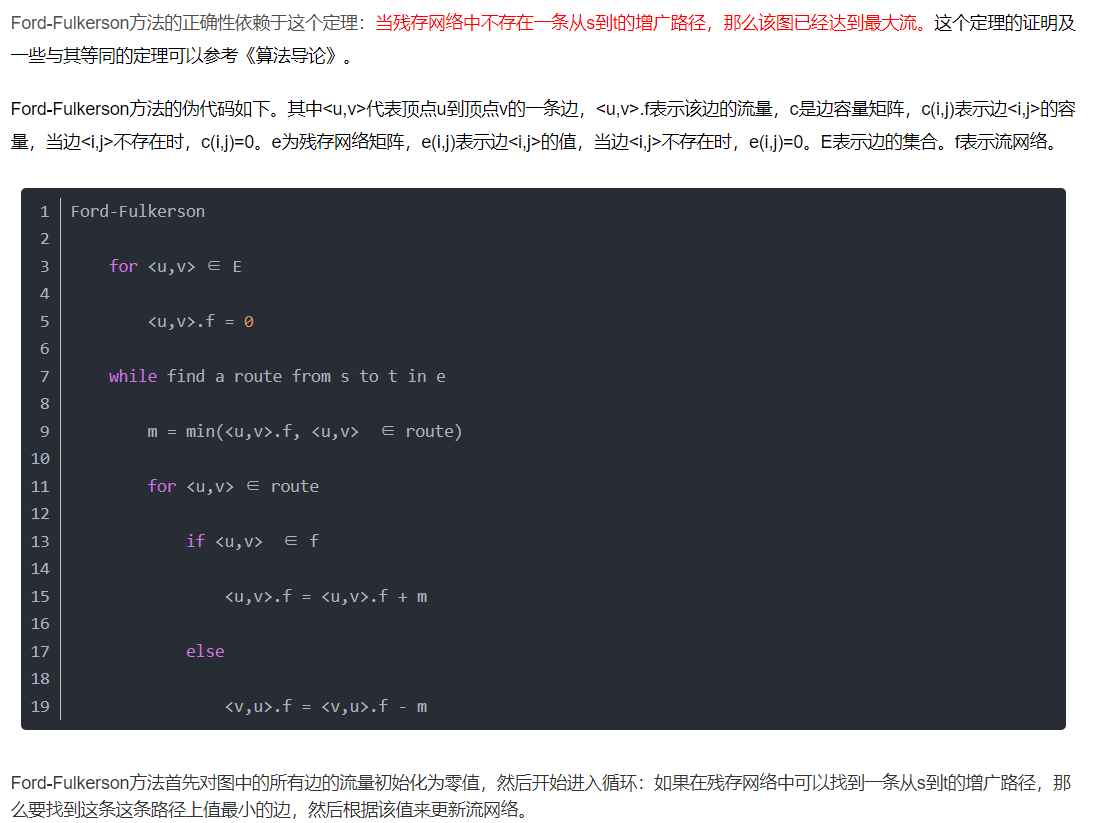
Ford-Fulkerson方法的基本思想:
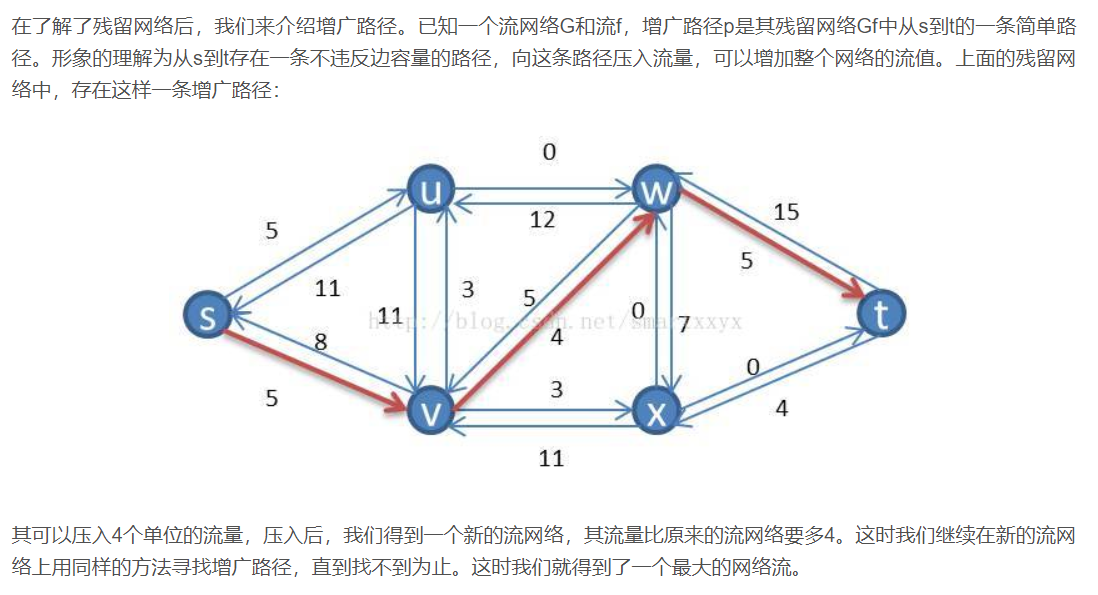
首先需要了解的是Ford-Fulkerson是一种迭代的方法。该方法依赖于三种重要思想:残留网络,增广路径和割。开始时,对所有的u,v属于V,f(u,v)=0(这里f(u,v)代表u到v的边当前流量),即初始状态时流的值为0。在每次迭代中,可以通过寻找一个“增广路径”来增加流值。增广路径可以看做是从源点s到汇点t之间的一条路径,沿该路径可以压入更多的流,从而增加流的值。反复进行这一过程,直到增广路径都被找出为止。
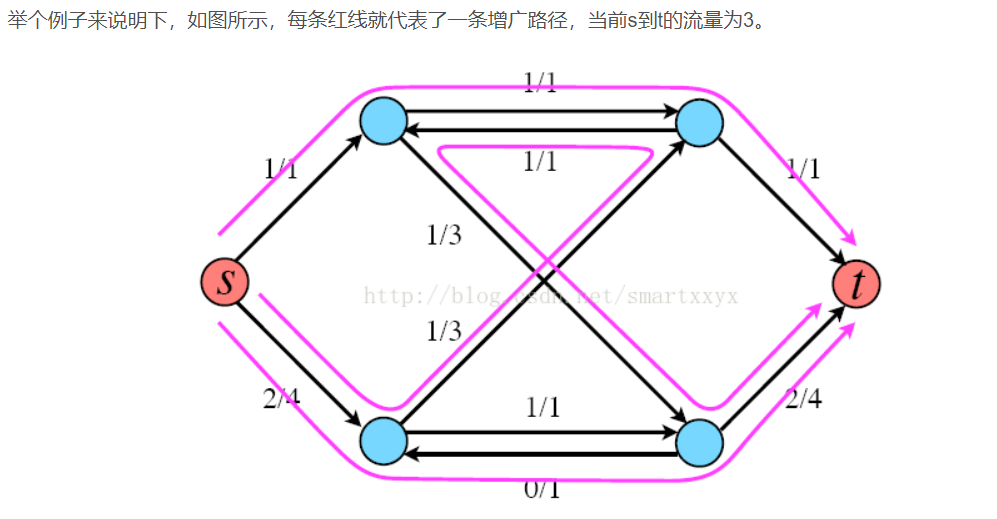
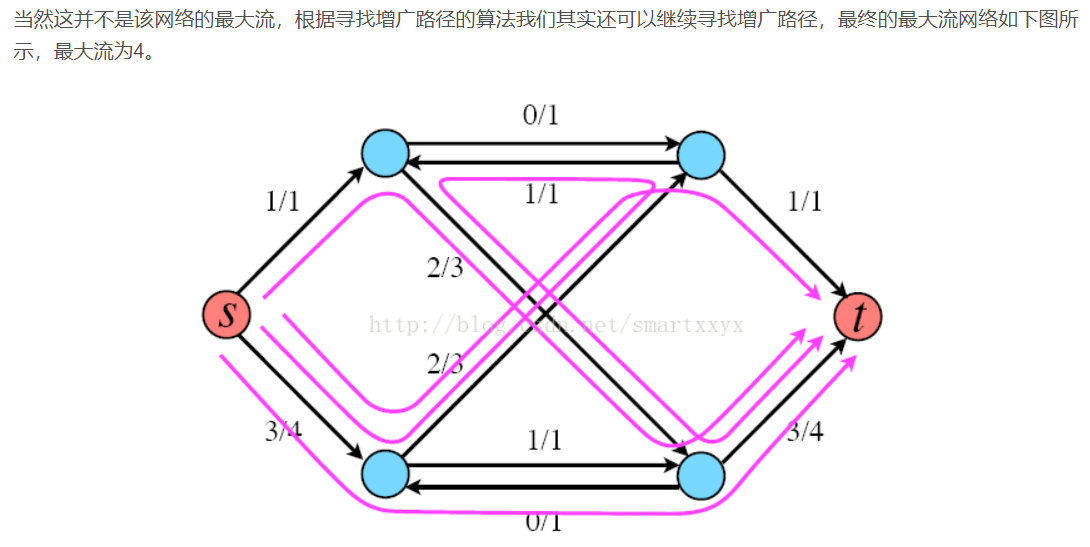
残留网络:

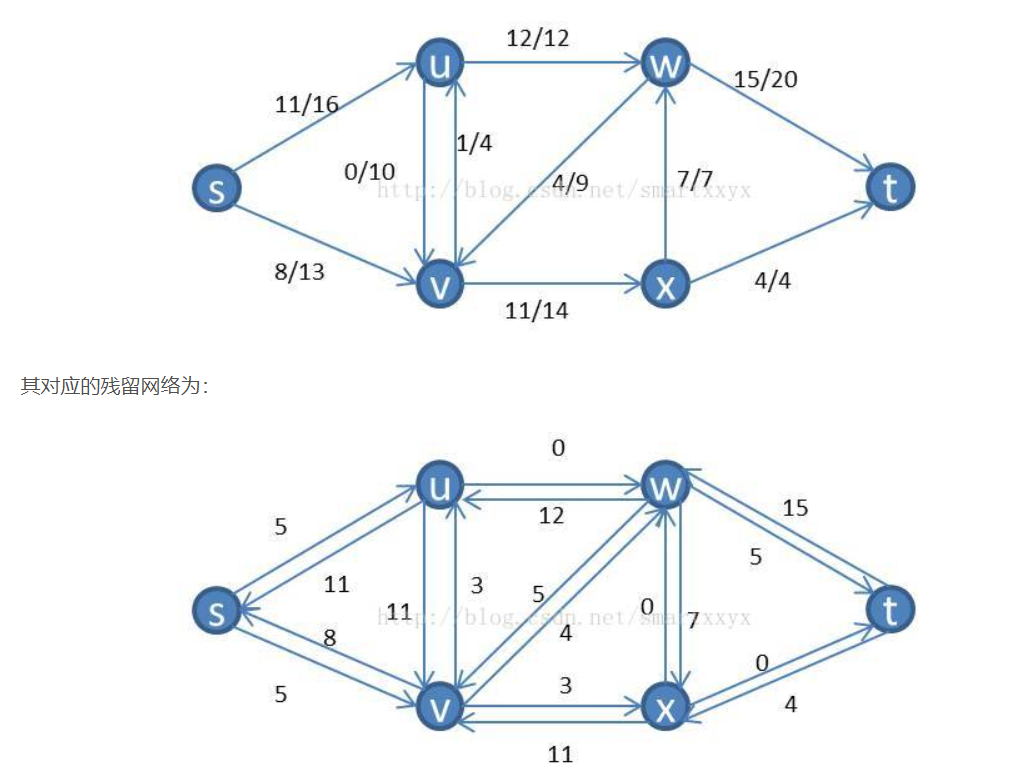
增广路经:
流网络的割:
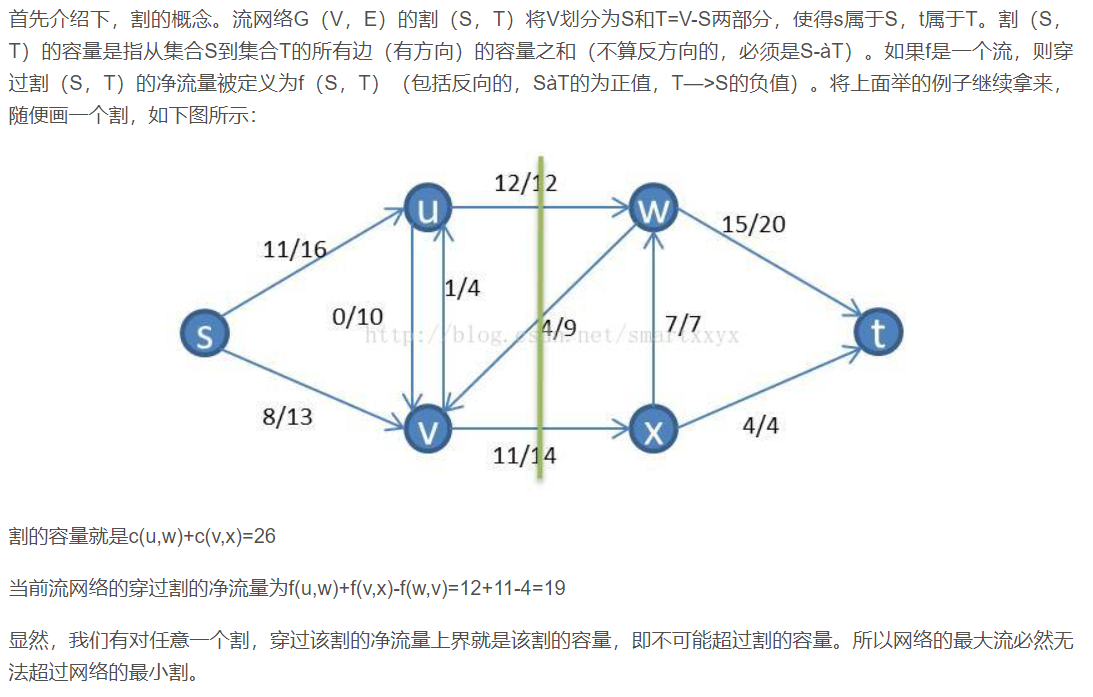
对网络的任意割,其净流量的都是相等的将s比喻成一个水龙头,u和v流向别处的水流,都是来自s的,其自身不可能创造水流。所以任意割的净流量都是相等的。
当残留网络Gf中不包含增广路径时,f是G的最大流
假设Gf中不包含增广路径也即s,t之间没有路径 那么集合S不包含t,(S,T)就符合割的定义; 假设T中有点v,与s有通路,那么与S的定义相矛盾; 那么对于(S,T)这个割,流量已经达到上限,故不能再增加流; 根据任意割的净流量都是相等的,不会存在有割流量比(S,T)大,且未达上限的情况。 故不存在增广路径时,最大流=最小割。
-
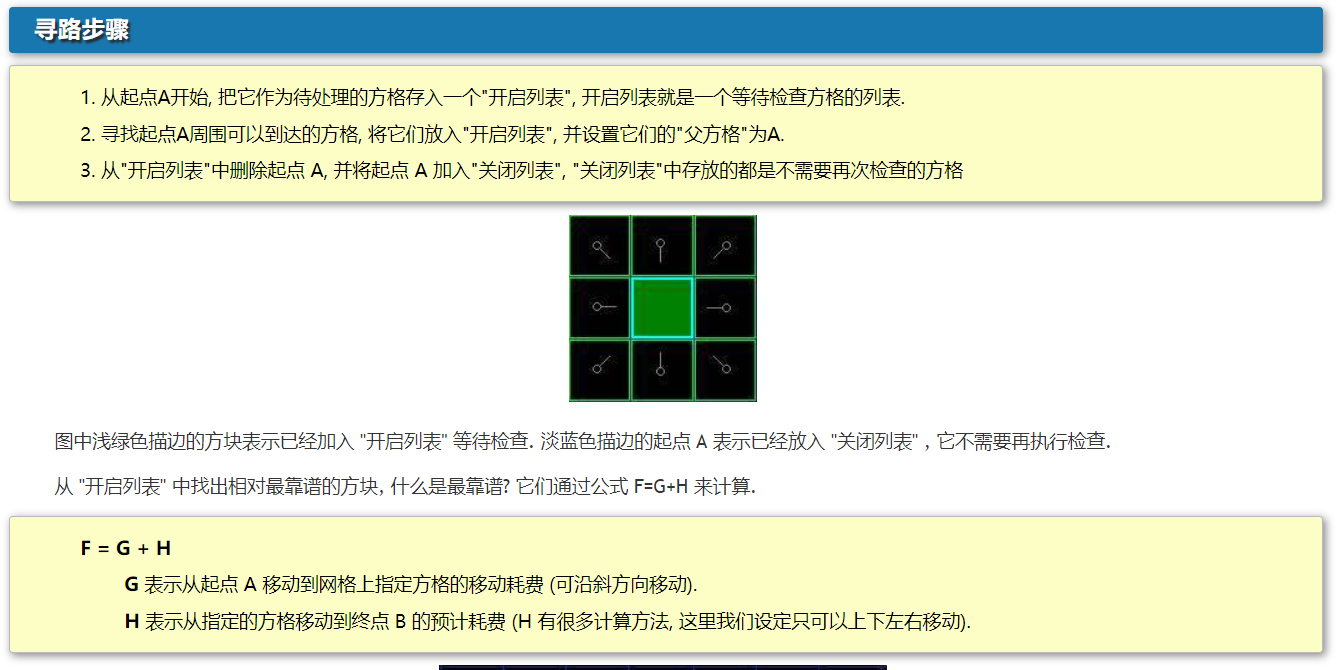
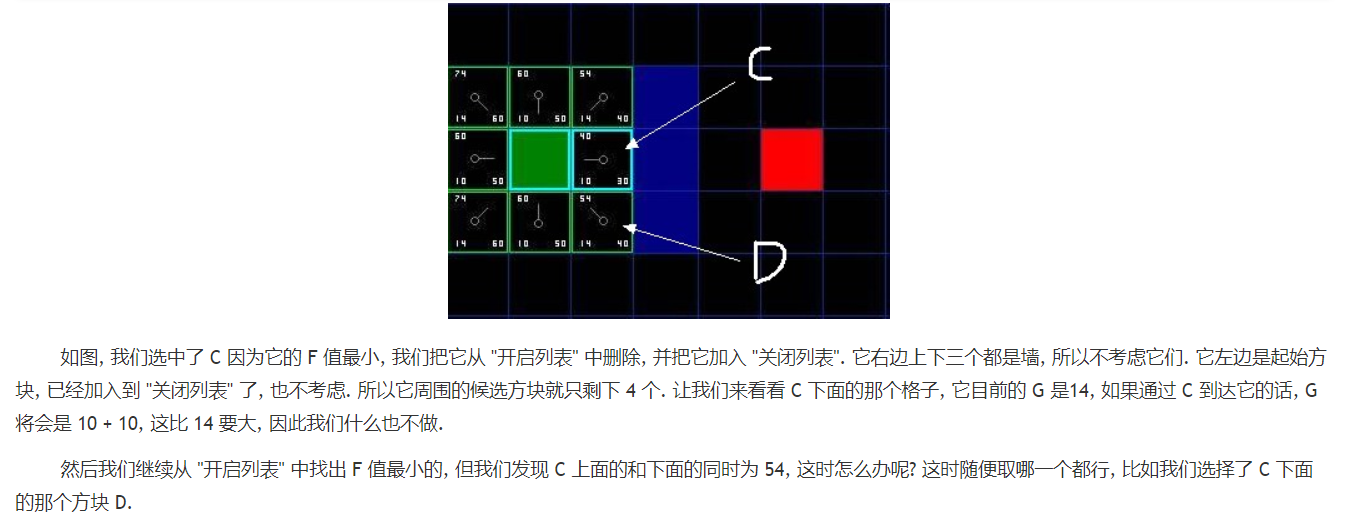
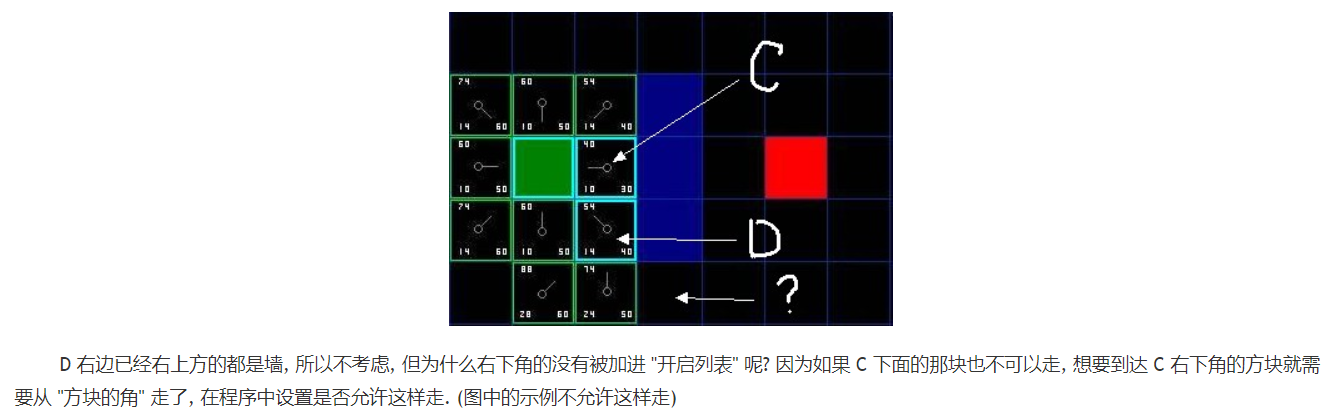
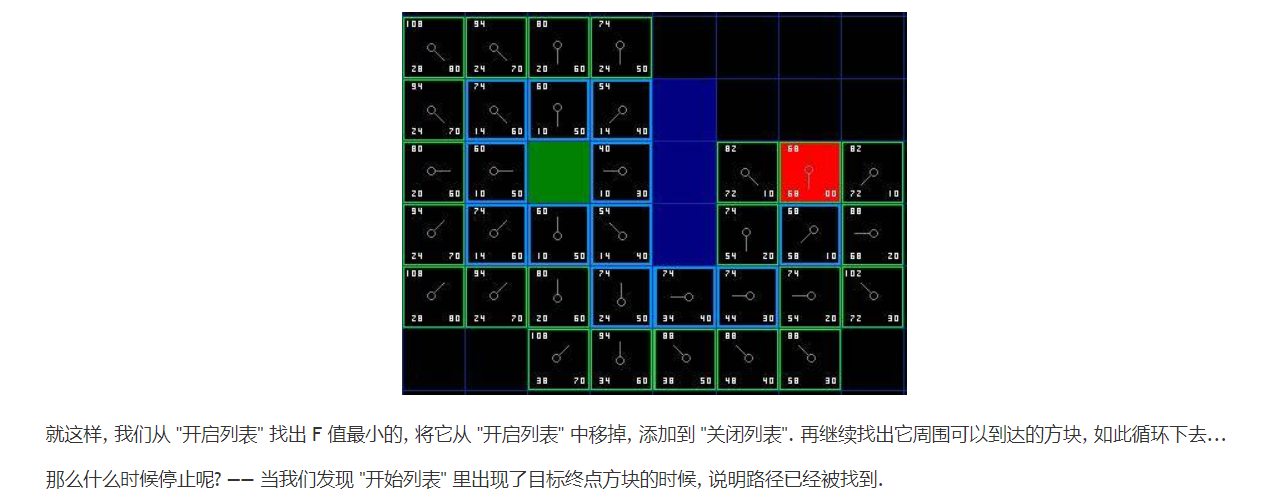
实战之A*搜索算法