散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
概念
散列表hashtable(key,value) 就是把Key通过一个固定的算法函数即散列函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里。通过散列算法,变换成固定长度的输出,该输出就是散列值。这种转换是一种压缩映射,简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
而当使用哈希表进行查询的时候,就是再次使用哈希函数将key转换为对应的数组下标,并定位到该空间获取value,如此一来,就可以充分利用到数组的定位性能进行数据定位。
why:
数组的特点是:寻址容易,插入和删除困难;
而链表的特点是:寻址困难,插入和删除容易。
散列表结合了两者的优势,寻址容易,插入删除也容易。
散列函数构造方法
-
直接定址法
关键码本身和地址之间存在某个线性函数关系时,散列函数取为关键码的线性函数,即:H(key)=a*key+b,a、b均为常数。
这样的散列函数优点就是简单、均匀,也不会产生冲突,但问题是这需要事先知道关键字的分布情况,适合査找表较小且连续的情况。由于这样的限制,在现实应用中虽然简单,但却并不常用。
-
除留余数法
通过选择适当的正整数p,按计算公式H(K)=K mod p来计算关键码K的散列地址。
若关键码个数为n,散列表表长为m(一般m>=n),通常选p为小于或等于表长m的最大素数或不包含小于20的质因子的合数,一般也要求p>=n。
这种方法计算最简单,也不需根据全部关键码的分布情况研究如何从中析取数据,最常用。
-
平方取中法
将关键码K平方,取K^2中间几位作为其散列地址H(K)的值。
假如有以下关键字序列{421,423,436},平方之后的结果为{177241,178929,190096},那么可以取{72,89,00}作为Hash地址。
-
随机数法
采用随机函数作为散列函数H(Key)=random(Key),其中random为随机函数。
当关键码长度不等时,采用该方法较恰当。
产生Hash冲突的处理方法
-
可以理解为“链表的数组”
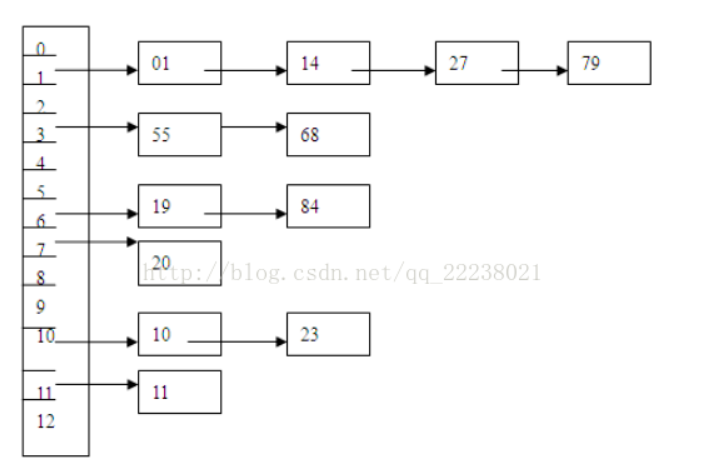
-
再哈希
-
缓冲区
建立一个缓冲区,把凡是Hash(key)重复的元素放到缓冲区中。当我通过key查找时,发现找的不对,就在缓冲区里找。
-
开放定址法
从发生冲突位置的下一个位置开始寻找空的散列地址。发生冲突时,线性探测下一个散列地址是:Hi=(H(key)+di)%m,(di=1,2,3…,m-1)
-
拉链法
具体的关键字列表为(19,14,23,01,68,20,84,27,55,11,10,79),则散列函数为H(key)=key MOD 13。则采用除留余数法和拉链法后得到的预想结果应
应用
Hash主要用于信息安全领域中加密算法,它把一些不同长度的信息转化成杂乱的128位的编码,这些编码值叫做Hash值. 也可以说,Hash就是找到一种数据内容和数据存放地址之间的映射关系。
查找:哈希表,又称为散列,是一种更加快捷的查找技术。我们之前的查找,都是这样一种思路:集合中拿出来一个元素,看看是否与我们要找的相等,如果不等,缩小范围,继续查找。而哈希表是完全另外一种思路:当我知道key值以后,我就可以直接计算出这个元素在集合中的位置,根本不需要一次又一次的查找,时间复杂度为O(1)。
Hash表在海量数据处理中有着广泛应用。
布隆过滤器
Bit-map空间压缩和快速排序去重
Bit-map的基本思想
32位机器上,对于一个整型数,比如int a=1 在内存中占32bit位,这是为了方便计算机的运算。但是对于某些应用场景而言,这属于一种巨大的浪费,因为我们可以用对应的32bit位对应存储十进制的0-31个数,而这就是Bit-map的基本思想。Bit-map算法利用这种思想处理大量数据的排序、查询以及去重。 Bitmap在
用户群做交集和并集运算的时候也有极大的便利。
- Bit-map应用之快速排序
假设我们要对0-7内的5个元素(4,7,2,5,3)排序(这里假设这些元素没有重复),我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数,我们就只需要8个Bit(1Byte),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0,对应位设置为1。
遍历一遍Bit区域,将该位是一的位的编号输出(2,3,4,5,7),这样就达到了排序的目的,时间复杂度O(n)。
优点: 运算效率高,不需要进行比较和移位; 占用内存少,比如N=10000000;只需占用内存为N/8=1250000Byte=1.25M。
缺点: 所有的数据不能重复。即不可对重复的数据进行排序和查找。
- Bit-map应用之快速去重
2.5亿个整数中找出不重复的整数的个数,内存空间不足以容纳这2.5亿个整数。 首先,根据“内存空间不足以容纳这2.5亿个整数”我们可以快速的联想到Bit-map。下边关键的问题就是怎么设计我们的Bit-map来表示这2.5亿个数字的状态了。其实这个问题很简单,一个数字的状态只有三种,分别为不存在,只有一个,有重复。因此,我们只需要2bits就可以对一个数字的状态进行存储了,假设我们设定一个数字不存在为00,存在一次01,存在两次及其以上为11。那我们大概需要存储空间几十兆左右。 接下来的任务就是遍历一次这2.5亿个数字,如果对应的状态位为00,则将其变为01;如果对应的状态位为01,则将其变为11;如果为11,,对应的转态位保持不变。 最后,我们将状态位为01的进行统计,就得到了不重复的数字个数,时间复杂度为O(n)。
- Bit-map应用之快速查询
同样,我们利用Bit-map也可以进行快速查询,这种情况下对于一个数字只需要一个bit位就可以了,0表示不存在,1表示存在。假设上述的题目改为,如何快速判断一个数字是够存在于上述的2.5亿个数字集合中。 同之前一样,首先我们先对所有的数字进行一次遍历,然后将相应的转态位改为1。遍历完以后就是查询,由于我们的Bit-map采取的是连续存储(整型数组形式,一个数组元素对应32bits),我们实际上是采用了一种分桶的思想。一个数组元素可以存储32个状态位,那将待查询的数字除以32,定位到对应的数组元素(桶),然后再求余(%32),就可以定位到相应的状态位。如果为1,则代表改数字存在;否则,该数字不存在。
- Bit-map扩展——Bloom Filter(布隆过滤器)
当一个元素被加入集合中时,通过k个散列函数将这个元素映射成一个位数组中的k个点,并将这k个点全部置为1。 有一定的误判率–在判断一个元素是否属于某个集合时,有可能会把不属于这个集合的元素误判为属于这个集合.因此,它不适合那些“零误判”的应用场合.在能容忍低误判的应用场景下,布隆过滤器通过极少的误判换取了存储空间的极大节省,是一种拿错误率换取空间的数据结构。 Bloom Filter使用k个相互独立的哈希函数(Hash Function),它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x,第i个哈希函数映射的位置hi(x)就会被置为1(1≤i≤k)。注:如果一个位置多次被置为1,那么只有第一次会起作用,后面几次将没有任何效果。 在判断y是否属于这个集合时,对y应用k次哈希函数,若所有hi(y)的位置都是1(1≤i≤k),就认为y是集合中的元素,否则就认为y不是集合中的元素。
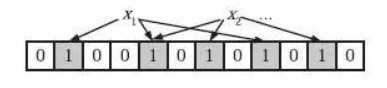
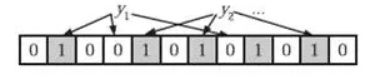
- 总结
布隆过滤器 (Bloom Filter)是一种space efficient的概率型数据结构,用于判断一个元素是否在集合中。在垃圾邮件过滤的黑白名单方法、爬虫(Crawler)的网址判重模块中等等经常被用到。散列表也能用于判断元素是否在集合中,但是布隆过滤器只需要散列表的1/8或1/4的空间复杂度就能完成同样的问题。布隆过滤器可以插入元素,但不可以删除已有元素。其中的元素越多,false positive rate(误报率)越大,但是false negative (漏报)是不可能的。